Die Ableitung 3

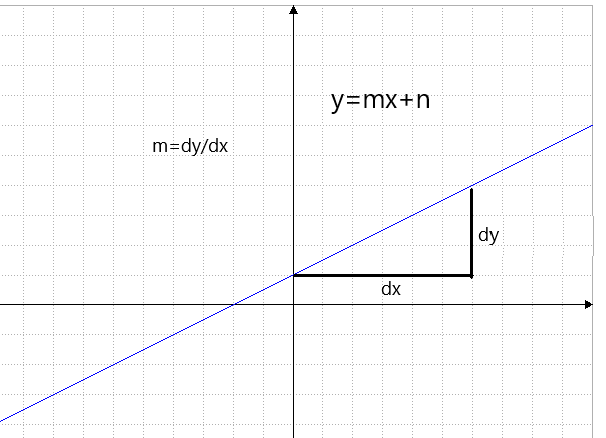
Ziel war die Steigung der Tangente
in P(2|4) an den Graphen von f(x)=x² .
Wir erhielten den Term für die Sekantensteigungen von links
m(h) = 4- h
Nun brauchen wir nur den letzten Schritt gehen:
h gegen 0 gehen lassen, damit die Punkte Q und P zusammenschmilzen.
Wir erhalten nun die Steigung in P(2|4), d.h. die Ableitung an der Stelle 2.
Die mathematische Schreibweise ist:
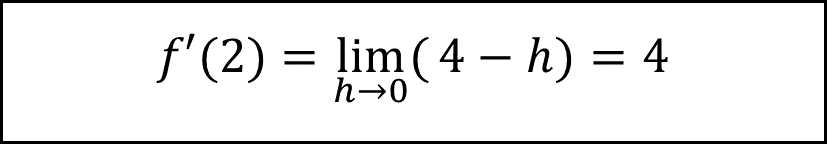Die Tangente lautet nun t: y= 4 x -4

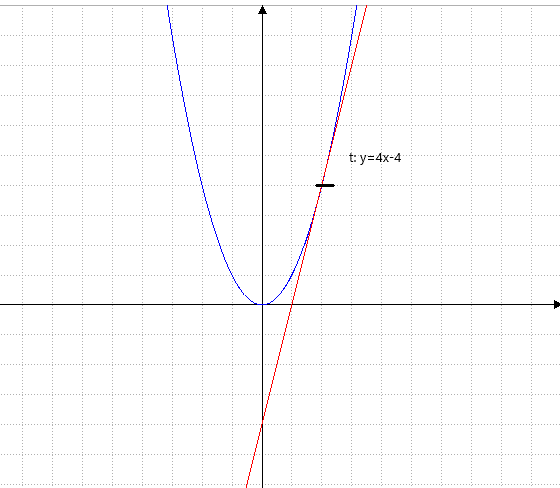
Nun können wir in jedem Punkt der Parabel auf diese Weise die Tangente berechnen.
Testen wir es einmal:

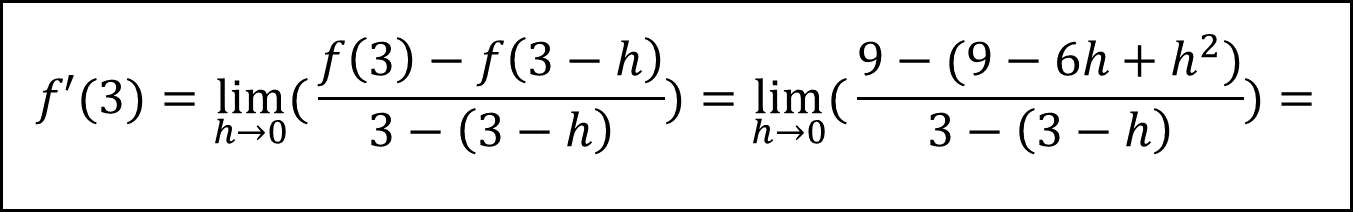
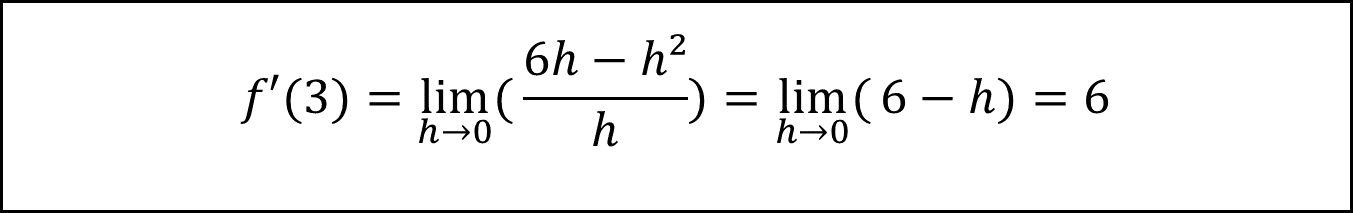Tangente berechnen:
P(3|9) und m einsetzen in y=mx+n
9= 6 * 3 + n also n=-9
t: y= 6x-9

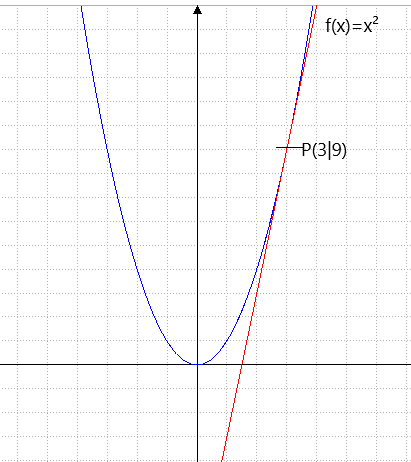
Sind wir jetzt fertig?
Nun das berechnen der Steigung in jedem einzelnen Punkt der Parabel macht schon etwas Arbeit.
Stellen wir uns das einmal für kompliziertere Funktionen vor!!
f(x)=x³-4x²+3x -7
Also ich habe keine Lust f(2-h) beispielsweise auszurechnen!!
Besser wir finden noch einen besseren Weg.
Der Weg ist steinig, bringt uns aber die Lösung der Probleme.
Also machen wir uns auf den Weg!

Wie sind wir bisher vorgegangen?
Wir haben einen konkreten Punkt genommen und dazu die Steigung der Tangente ausgerechnet.

Nun abstrahieren wir weiter, wir legen keinen festen Punkt zugrunde, sondern wir verwenden wieder Variablen.
Unser Punkt sei P(x|f(x)) auf dem Graphen von f(x)=x²

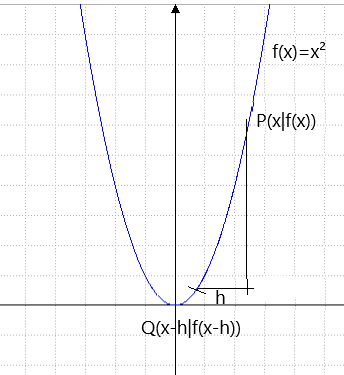
Die Steigung in diesem Punkt rechnen wir aber genau wie vorher aus:
wir nehmen einen Punkt links von P(x|f(x)) das ist Q(x-h|f(x-h)) h>0
Das wird anstrengend!
Hier die Gebrauchsanweisung:
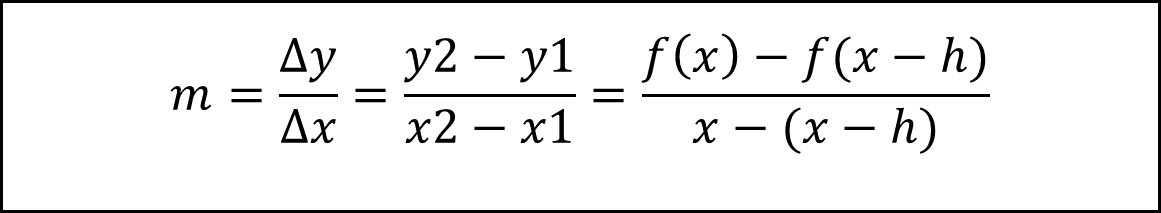Dieses komische Dreieck nennt man delta. Es steht als Abkürzung für Differenz.
Also merken: Differenz der y-Werte durch Differenz der x-Werte das ergibt die Steigung.
Das wissen wir doch längst!