Anwendungen der Ableitung: Tangenten
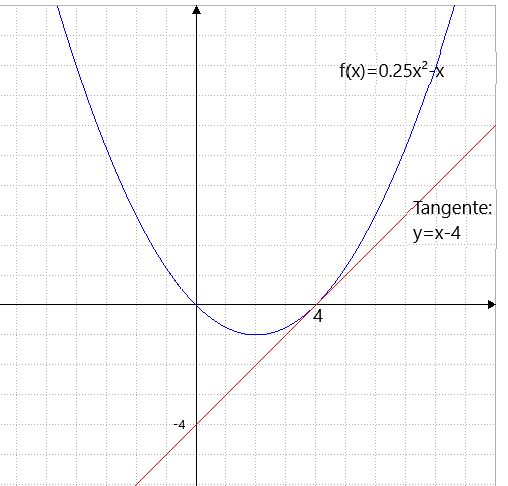
Berechne die Tangente in x=4 an die Parabel f(x)= 0.25 x²-x
Lösung
Was brauchen wir für die Tangente?
Wir brauchen den Punkt und die Steigung von f in diesem Punkt.
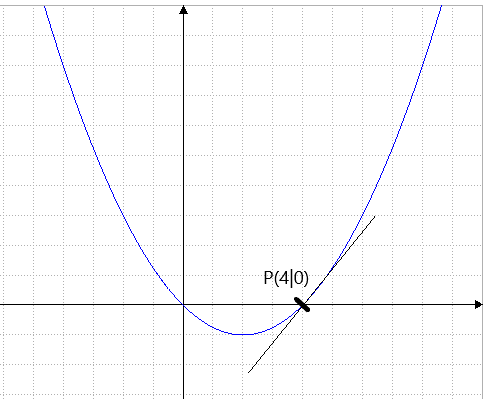
Es ist P(4|0)
f(x)=0.25x²-x
f(4)= 0.25 * 4² - 4 =0
und f'(4)=?
Nach den Ableitungsregeln ist
f'(x)= 0.5 x - 1
f'(4)= 0.5*4 -1 = 1
Also haben wir die Zutaten für eine Gerade:
m= 1 x=4 y=0 einsetzen in y=mx+n
0= 1 * 4 + n
n= -4
also Tangente: y=1x-4
fertig!
jetzt bitte selbst lösen!
Lösung
Lösung:
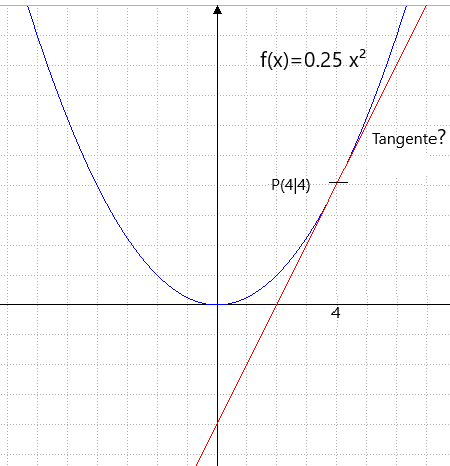
f(x)=0.25x² P(4|4)
f'(x)=0.5 x
f'(4)= 2
m=2 x=4 y= 4
4= 2* 4 +n
n=-4
Tangente:
y= 2x -4
f(x)=0.25x² P(4|4)
f'(x)=0.5 x
f'(4)= 2
m=2 x=4 y= 4
4= 2* 4 +n
n=-4
Tangente:
y= 2x -4