Berechne Hoch- und Tiefpunkte der Funktion
f(x)= 0.25 x³ -4 x

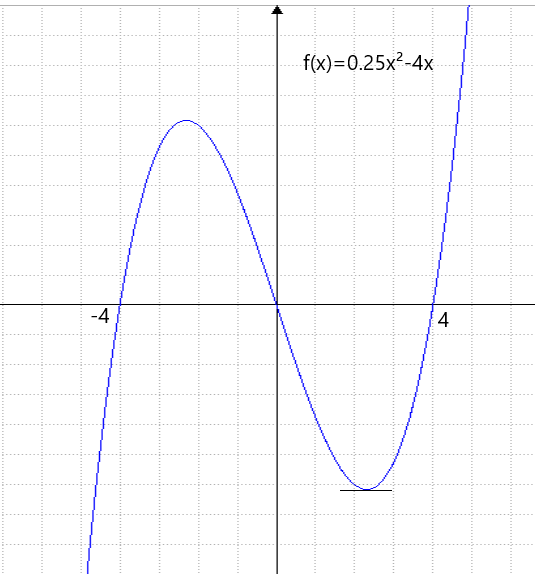
Da in den Hoch- und Tiefpunkten eine waagerechte Tangente vorliegt, Suchen wir wieder zunächst die Nullstellen der Ableitung f'
f(x)= 0.25 x³ -4 x

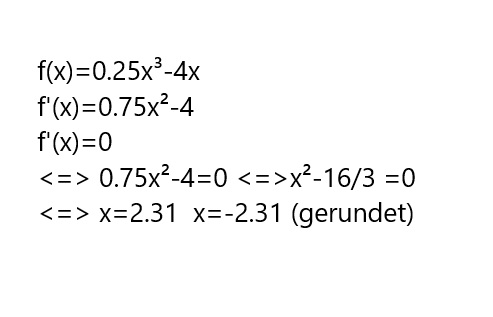
Wir erkennen an der Skizze, dass bei x=2.31 der Tiefpunkt ist und bei x=-2.31 ist der Hochpunkt.
Wenn wir aber den Graphen nicht vor uns sehen, brauchen wir noch weitere Kriterien.

Schauen wir uns die Steigung in der Umgebung des Tiefpunktes an.
links von der Stelle x=2.31 fällt die Kurve, rechts davon steigt sie wieder.

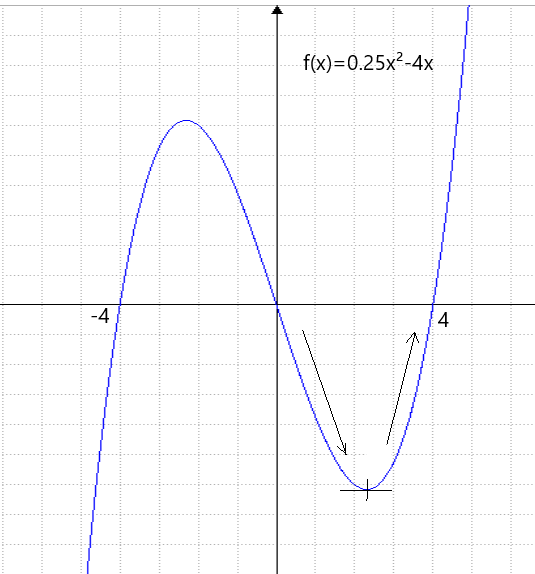
Das bedeutet die Ableitung verhält sich in der Umgebung von 2.31 ansteigend. Sie verläuft von negativ über 0 zu positiv.

Nun kann man von der Ableitung wieder eine Ableitung machen und prüfen, ob sie an der Stelle 2.31 postiv ist. 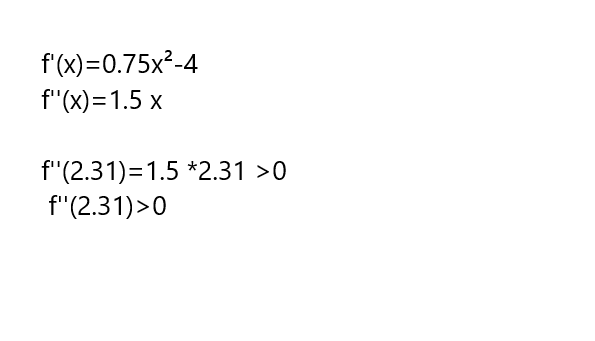Verfahre entsprechend für den Hochpunkt.