Die Ableitung 2

Die Lösung: m=3
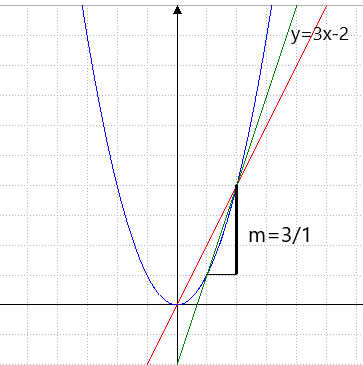
Sekante durch (1|1) und (2|4):
m=(4-1)/(2-1)=3/1=3
Diese Sekante ist schon eine bessere Näherung, wie man sieht. Wir sind auf dem richtigen Weg. Wir müssen jetzt mit dem Punkt links uns weiter annähern:
Auftrag 3:
Steigung durch (1,5|2,25) und (2|4) berechnen.

Lösung:
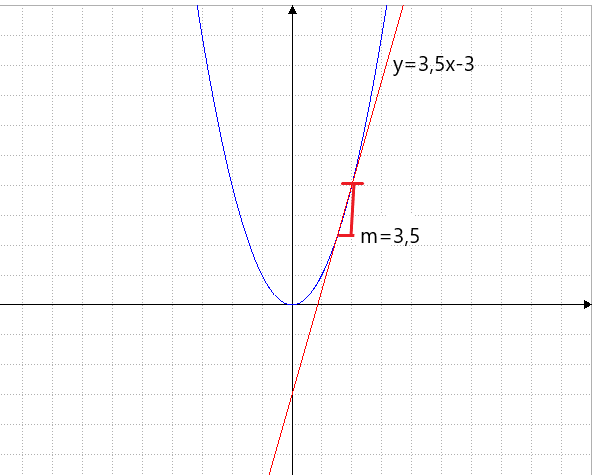
Sekante durch (1,5|2,25) und (2|4) :
m=(4-2,25)/(2-1,5)=1,75/0,5=3,5

Nun wird deutlich was passiert:
1. m=2
2. m=3
3. m=3,5 noch eine?
Autrag 4:
Steigung durch (1,9|3,61) und (2|4)

Lösung: m=3,9 geschafft? super!

So müssten wir jetzt weitermachen.
Das wird viel Arbeit !
Besser wir überlegen uns eine neue Strategie.
Es geht darum den Punkt links von (2|4) gar nicht konkret anzugeben, nur zu sagen er soll links Von (2|4) sein.
Links von 2 bedeutet 2-h (irgendein h>0)

Natürlich ist das etwas komplizierter, wird uns aber zum Ziel führen.

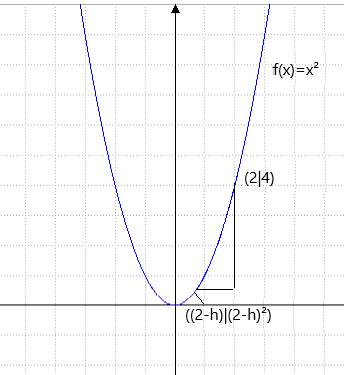
Unser Punkt links von (2|4) lautet also:
Q((2-h)| (2-h)²) denn f(x)=x², wenn man hier 2-h ensetzt ergibt das (2-h)²
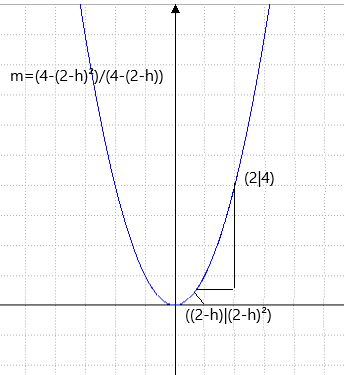
Nun trauen wir uns an die Steigung:
m=(4- (2-h)²)/(2-(2-h)) oh je!
Auftrag:
Löse diesen Term auf und vereinfache ihn!
(bin. Formel ! und Minuszeichen beachten! viel Glück!)

Lösung:
m=(4- (2-h)²)/(2-(2-h))
=(4-(4-4h+h²))/h
=(4h-h²)/h
durch h kürzen:
m= 4-h
war doch leicht oder?
Vergleicen wir mit unseren bereits berechneten Werten:
1. m=2 h=2 eingesetzt in 4-h ergibt auch 2.
2. m=3 h=1 ergibt tatsächlich m=3
3. m=3,5 h=0,5 eingesetzt in 4-h ergibt 0,5
Unser Term für die Steigung ist gut!