Die Ableitung

Die Ableitung ist eine Funktion f', die für jeden Punkt der Ausgangsfunktion f die Steigung in diesem Punkt angibt.
Am besten wir schauen uns ein Beispiel an.
Gegeben sei die Funktion f(x)=2x-3
Der Graph von f ist eine Gerade.
Diese Gerade hat die Steigung 2.
Das bedeutet, daß der Graph um 2 Einheiten nach oben steigt, wenn man eine Einheit nach rechts geht. Dies kann man im Bild gut erkennen, wenn man z.B. vom Punkt (0|-3) zum Punkt (1|-1) geht.

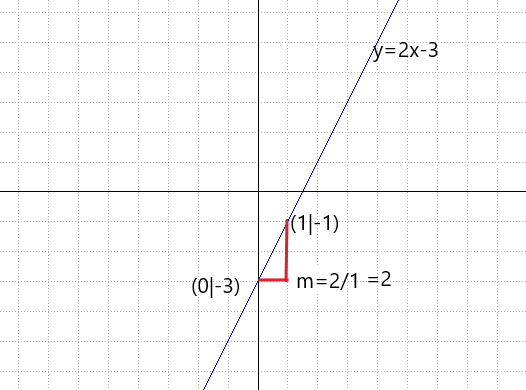
Diese Gerade y=2x-3 hat nun in jedem Punkt die gleiche Steigung, weil sie eine lineare Funktion ist.
Es ist also leicht in jedem Punkt ihre Steigung anzugeben, sie ist 2.

Die Ableitungsfunktion hat dann die Gleichung y=2.
Besser ausgedrückt:
f(x)=2x-3 Die Ableitung lautet: f'(x)=2
Das war doch einfach oder?

Dies kann man sogar für alle Geraden so festlegen:

Wenn wir eine Gerade f gegeben haben, so kennen wir schon ihre Ableitungsfunktion f' .
Für f(x)= m x +n ist die Ableitung f'(x)= m, denn m ist ja die Steigung jeder Geraden.

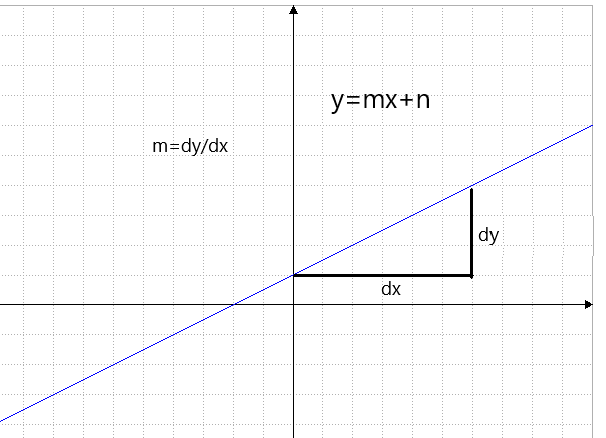
Nun wird es komplizierter, aber nicht verzweifeln!
Wir schaffen das schon.
Nehmen wir uns nun eine Parabel vor: f(x)=x²
Wie kann man die Steigung hier ablesen? Am besten man stellt sich vor, dass man ein Lineal in einem Punkt anlegt und so in etwa die Steigung ablesen kann (??) Beispiel kommt sofort!

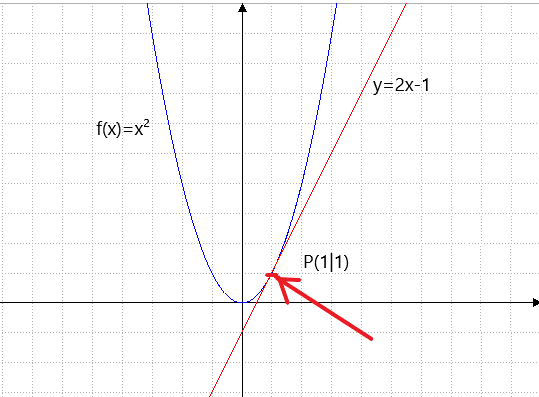
An der Stelle (1|1) ist eine Tangente gezeichnet mit der Steigung 2.
Daß es genau 2 ist, können wir allerdings bisher nur raten. Man bräuchte eigentlich nur für jeden Punkt der Parabel die passende Tangente finden... Na ja, ist aber nicht so leicht.
Es ist schon eine geniale Erfindung gewesen, die Sache mit der Ableitung.

Machen wir uns an die Arbeit:
Wir müssen irgendwie an die Tangente im Punkt P(2|4) kommen!
Da behelfen wir uns doch am besten mit einer Annäherung:
(das macht man in der Mathematik öfters!)
Haben wir keine Tangente, dann nehmen wir eben eine Sekante, die können wir exakt berechnen.
Autrag 1:
Bestimme die Steigung der Sekante durch (0|0) und (2|4) für die Parabel y=x²

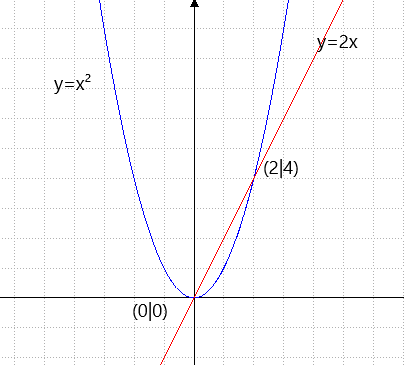
und geschafft?
Die Steigung:
m=(4-0)/(2-0)=4/2=2 (viel zu leicht!)
Leider sind wir noch lange nicht fertig ! Mühsam ernährt sich das Eichhörnchen... Habt ihr gemerkt, Daß ich schon alles verraten hatte?
Oben stand es schon:
Die Gleichung der Sekante ist y=2x, also m=2 .

Jetzt wollen wir ein Ziel festlegen.
Ziel: Tangente in (2|4) herausfinden. Dazu benutzen wir die Annäherung über Sekanten.
Dies kann links von P(2|4) oder rechts davon ausgehen. Wir nehmen diesmal Punkte von links und nähern uns dem Punkt P(2|4) an.
Die erste Näherung haben wir ja schon m=2! Aber die Steigung der Tangente muss größer als 2 sein. Das sieht man.
Auftrag 2:
Steigung der Sekante durch (1|1) und (2|4) ausrechnen und einzeichnen.